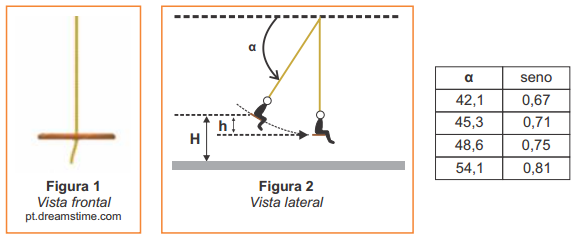
Um aluno resolve colocar em prática seus conhecimentos de Física enquanto brinca com os colegas em um balanço de corda única de comprimento L (figura 1). Ele deseja que, ao passar pelo ponto mais baixo da trajetória, a tração na corda corresponda a 3/2 de seu peso. Após alguns cálculos, ele, depois de sentar-se no balanço, pede para que um colega posicione o balanço conforme indicado na figura 2. Considerando desprezíveis todas as formas de atrito e que, no início do movimento, o balanço está com a corda esticada, parte do repouso e descreve uma trajetória circular, qual o ângulo α encontrado por ele?
a) 42,1
b) 45,3
c) 48,6
d) 54,1
Resposta: C
A partir dos dados do enunciado e da figura fornecida, pode-se desenhar o esquema a seguir:
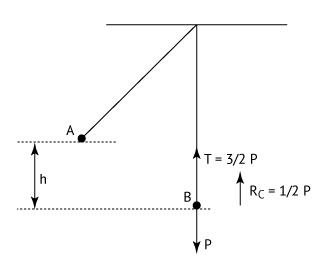
A resultante das forças no ponto mais baixo da trajetória é centrípeta e é calculada como a diferença entre a tração no fio e o peso do corpo. Assim:
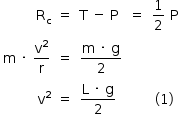
Considerando desprezíveis todas as formas de atrito e que, no início do movimento, o balanço está com a corda esticada e parte do repouso, tem-se:
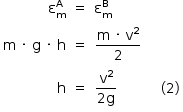
Substituindo-se 1 em 2,
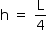
A partir desse resultado, pode-se desenhar o esquema a seguir:

Como os ângulos α e β são complementares, cosβ = senα. Logo:
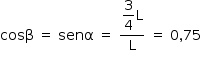
Assim, consultando a tabela, o valor de α é 48,6°.
