Um veículo percorre a distância entre duas cidades de tal forma que, quando percorre a primeira metade desse trajeto com velocidade constante e igual a 15 m/s, gasta 2h a mais do que quando o percorre, também com velocidade constante e igual a 25 m/s. A segunda metade desse trajeto é sempre percorrido com velocidade constante e igual à média aritmética das duas velocidades anteriores. Nestas condições, quando o veículo percorrer a primeira metade do trajeto com velocidade constante de 25 m/s, a velocidade média, em km/h, ao longo de todo o trajeto, a distância, em km, entre as cidades e o tempo gasto, em h, na primeira metade do trajeto quando a velocidade vale 15 m/s valem, respectivamente,
a) 40, 270 e 2,5
b) 40, 270 e 4,5 c) 80, 540 e 5,0
d) 80, 540 e 3,0
Resposta: C
Para a solução dessa questão deve-se adotar:
- V1 = 25 m/s = 90 km/h (velocidade em que o tempo de percurso é t)
- Δt 1 = t
- V2 = 15 m/s = 54 km/h (velocidade em que o tempo de percurso possui 2 h a mais)
- Δt 2 = t + 2
O percurso percorrido com essas duas velocidades é a metade do percurso total (ΔSTOTAL = 2x); assim, para metade do percurso será ΔS = x.
Aplicando-se a definição de velocidade escalar média para as duas velocidades, tem-se:
90 = x/t → x = 90 · t (I)
54 = x/(t +2) → x = 54 · (t +2) (II)
Igualando-se (I) e (II), tem-se: t = 3 h
Devolvendo t na equação (I):
x = 270 km e, portanto, o percurso total terá 540 km.
A velocidade média informada do segundo percurso é a média aritmética das duas velocidades. Assim:
Vm2 = (V1 + V2)/2 = (90 + 54)/2 = 72 km/h
O tempo para a outra metade do percurso será:
72 = 270/Δt’ → Δt’=(270/72) h
Logo, a velocidade ao longo de todo o trajeto com o primeiro trecho com velocidade 25 m/s será:
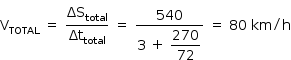
O tempo gasto na primeira metade com velocidade de 15 m/s será:
Δt 2 = t + 2 = 3 + 2 = 5 h
