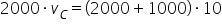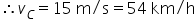Uma caminhonete, de massa 2.000 kg, bateu na traseira de um
sedã, de massa 1.000 kg, que estava parado no semáforo, em
uma rua horizontal. Após o impacto, os dois veículos deslizaram
como um único bloco. Para a perícia, o motorista da
caminhonete alegou que estava a menos de 20 km/h quando o
acidente ocorreu. A perícia constatou, analisando as marcas de
frenagem, que a caminhonete arrastou o sedã, em linha reta,
por uma distância de 10 m. Com este dado e estimando que o
coeficiente de atrito cinético entre os pneus dos veículos e o
asfalto, no local do acidente, era 0,5, a perícia concluiu que a
velocidade real da caminhonete, em km/h, no momento da
colisão era, aproximadamente,
Note e adote:
Aceleração da gravidade: 10 m/s².
Desconsidere a massa dos motoristas e a resistência do ar.
a) 10.
b) 15.
c) 36.
d) 48.
e) 54.
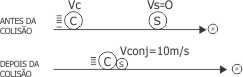
As forças aplicadas no conjunto caminhonete (C) e sedã (S), após a colisão, são
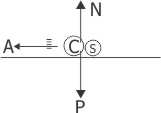
Como a normal equilibra o peso:
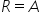
Utilizando o princípio fundamental da dinâmica:
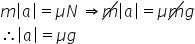
Sendo 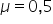 e
e 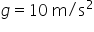 :
:
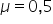 e
e 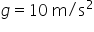 :
: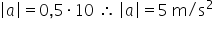
Dessa maneira, a velocidade do conjunto logo após a colisão pode ser obtida por meio da equação de Torricelli:
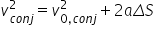
Sendo 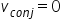 ,
, 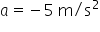 e
e 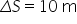 :
:
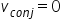 ,
, 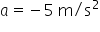 e
e 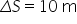 :
: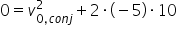
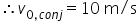
Agora, para se obter a velocidade com que a caminhonete colidiu com o sedã, basta lembrar que a colisão, que é inelástica, é um sistema isolado
:

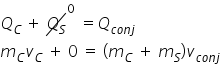
Sendo 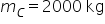 e
e 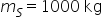 :
:
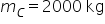 e
e 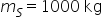 :
: