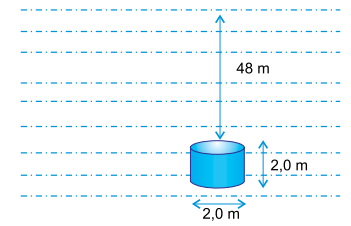
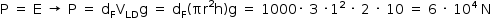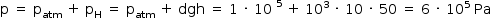Para determinados tipos de pesquisa ou trabalho, cápsulas tripuladas são enviadas para as profundezas dos oceanos, mares ou lagos. Considere uma dessas cápsulas de forma cilíndrica, de 2,0 m de altura por 2,0 m de diâmetro, com sua base superior a 48 m de profundidade em água de densidade 1,0.103 kg/m3, em equilíbrio como ilustra a figura.
Dados: A pressão atmosférica no local é de 1,0.105 Pa, e a aceleração da gravidade é de 10 m/s2. Adote π = 3.
O peso dessa cápsula fora d’água, em N, e a pressão total sobre sua base inferior, em Pa, valem, respectivamente,
a) 1,5.103 e 5,0.106.
b) 1,5.103 e 6,0.105.
c) 1,5.104 e 5,0.106.
d) 6,0.104 e 6,0.106.
e) 6,0.104 e 6,0.105.
c) 1,5.104 e 5,0.106.
d) 6,0.104 e 6,0.106.
e) 6,0.104 e 6,0.105.