(FGV-SP 2016) - QUESTÃO

Uma pedra de gelo, de 1,0 kg de massa, é retirada de um ambiente em que se encontrava em equilíbrio térmico a –100 ºC e recebe 150 kcal de uma fonte de calor. Considerando o calor específico do gelo 0,5 cal/(g.ºC), o da água 1,0 cal/(g.ºC), e o calor latente de fusão do gelo 80 cal/g, o gráfico que representa corretamente a curva de aquecimento dessa amostra é:

a) 

b)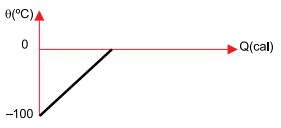 

c)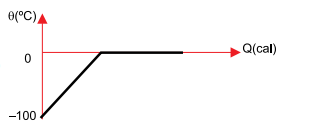 

d)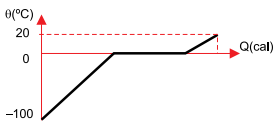 

e)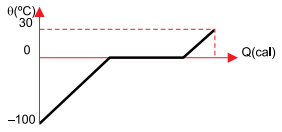 

                                                                                                                             Resposta: D

De acordo com o enunciado, dispomos de 150 kcal (150 000 cal) para fornecer energia para a amostra. Essa energia será capaz de:

1. aquecer a amostra de gelo de –100º C até 0º C:

2. realizar a mudança de estado físico da amostra:

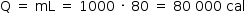
3. aquecer a amostra até a temperatura final X, pois restam 20 000 cal

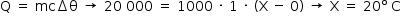
Assim, o gráfico que corresponde à situação descrita é dado pela alternativa D.