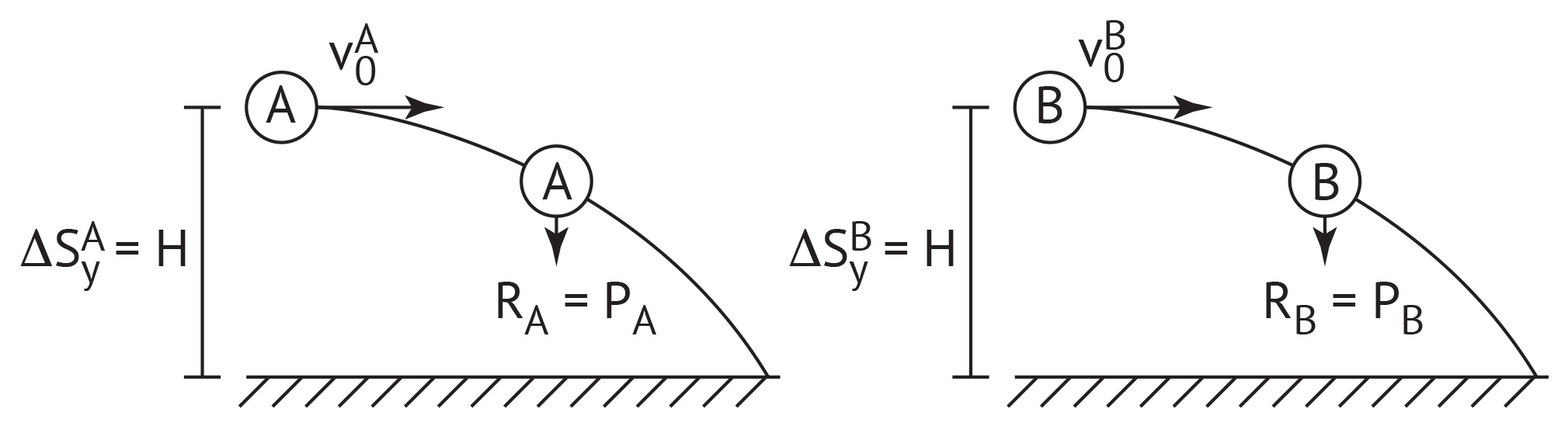
Para um salto no Grand Canyon usando motos, dois paraquedistas vão utilizar uma moto cada, sendo que uma delas possui massa três vezes maior. Foram construídas duas pistas idênticas até a beira do precipício, de forma que no momento do salto as motos deixem a pista horizontalmente e ao mesmo tempo. No instante em que saltam, os paraquedistas abandonam suas motos e elas caem praticamente sem resistência do ar.
As motos atingem o solo simultaneamente porque
a) possuem a mesma inércia.
b) estão sujeitas à mesma força resultante.
c) têm a mesma quantidade de movimento inicial.
d) adquirem a mesma aceleração durante a queda.
e) são lançadas com a mesma velocidade horizontal.
Resposta comentada (d)
O movimento descrito pelas motos é a composição de dois movimentos que ocorrem simultaneamente; na horizontal (movimento uniforme) e na vertical (queda livre), pois a única força que age em cada uma delas é seu próprio peso. Logo:
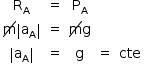
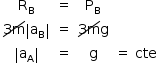
Como as motos perderam o contato com as pistas (que possuem mesma altura) no mesmo instante, e na vertical o movimento é uniformemente acelerado (queda livre), podemos calcular o tempo de queda de cada uma delas:
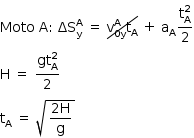
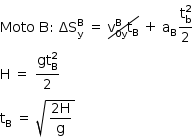
Assim, o tempo de queda das motos é o mesmo, independente de suas massas e de suas velocidades horizontais.
