Considere um sistema formado por duas cordas elásticas diferentes, com densidades lineares µ1 e µ2 , tal que µ1 > µ2. Na corda de densidade linear µ1 é produzido um pulso que se desloca com velocidade constante e igual a v, conforme indicado na figura abaixo. Após um intervalo de tempo Δt, depois de o pulso atingir a junção das duas cordas, verifica-se que o pulso refratado percorreu uma distância 3 vezes maior que a distância percorrida pelo pulso refletido. Com base nessas informações, podemos afirmar, respectivamente, que a relação entre as densidades lineares das duas cordas e que as fases dos pulsos refletido e refratado estão corretamente relacionados na alternativa:
a) µ1 = 3.µ2, o pulso refletido sofre inversão de fase mas o pulso refratado não sofre inversão de fase.
b) µ1= 3.µ2 , os pulsos refletido e refratado não sofrem inversão de fase.
c) µ1 = 9.µ2 , o pulso refletido não sofre inversão de fase mas o pulso refratado sofre inversão de fase.
d) µ1 = 9.µ2, os pulsos refletido e refratado não sofrem inversão de fase.
Resposta: D
Como, em um mesmo intervalo de tempo, o pulso refratado percorreu uma distância 3 vezes maior que o pulso refletido, podemos inferir que a velocidade de propagação do pulso na corda 2 é 3 vezes maior que a velocidade do pulso na corda 1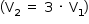 
.
.
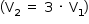Uma vez que a velocidade de propagação de um pulso em uma corda é dada por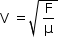 
, em que F é a força de tração nas cordas (igual para ambas) e µ, a densidade linear da corda. Tem-se:
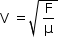, em que F é a força de tração nas cordas (igual para ambas) e µ, a densidade linear da corda. Tem-se: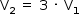
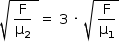
Procedendo-se às devidas operações algébricas: µ1 = 9 · μ2
Sendo a velocidade de propagação da corda 1 menor que na corda 2, pode-se afirmar que, para esse pulso, a corda 1 é um meio mais refringente.
Dessa forma, o pulso é refratado de um meio mais refringente a outro menos refringente.
Nessa circunstância, o pulso refletido e o pulso refratado não são submetidos à inversão de fase.