(MACKENZIE 2016) - QUESTÃO

Considere quatro lentes esféricas delgadas de distância focal f1 = +5,0 cm, f2 = -10,0 cm, f3 = +20,0 cm e f4 = - 40,0 cm. 

A justaposição de duas lentes terá a maior convergência quando associarmos as lentes 

a) 1 e 2 

b) 2 e 3 

c) 1 e 3 

d) 2 e 4 

e) 1 e 4

---------------------------------------------------------------------- RESPOSTA: C

A convergência ou vergência (C) da lente é definida por:

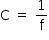
Em dioptrias (di), as convergências das lentes fornecidas são:

• Lente 1: 
  
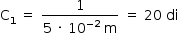
• Lente 2:
  
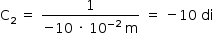
• Lente 3:
  ​
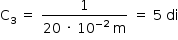
• Lente 4:
  

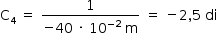
Em uma associação por justaposição, a convergência da lente equivalente é dada pela soma das convergências das lentes associadas.
Assim, para cada caso proposto nas opções, tem-se:

a) Lentes 1 e 2: C12 = C1 + C2 = 20 + (–10) = 10 di
b) Lentes 2 e 3: C23 = C2 + C3 = –10 + 5 = 5 di
c) Lentes 1 e 3: C13 = C1 + C3 = 20 + 5 = 25 di
d) Lentes 2 e 4: C24 = C2 + C4 = –10 + (–2,5) = –12,5 di
e) Lentes 1 e 4: C14 = C1 + C4 = 20 + (–2,5) = +17,5 di

Nota-se que a maior convergência aparece na associação 1 e 3 (opção C).